Các dạng toán về hình chữ nhật – Toán lớp 8 – Trường Quốc Học
Mục Lục
Toán cấp 2 nhắc lại lý thuyết về hình chữ nhật cùng các dạng toán liên quan với những bài tập có lời giải. Giúp các em lớp 8 ôn tập bồi dưỡng tốt.
Mục tiêu:
– Giúp học viên nắm được định nghĩa hình chữ nhật, những đặc thù của hình chữ nhật, những tín hiệu phân biệt một tứ giác là hình chữ nhật .– Học sinh biết vẽ hình chữ nhật, biết chứng tỏ một tứ giác là hình chữ nhật, biết vận dụng những kỹ năng và kiến thức về hình chữ nhật để giải toán .
– Rèn cho học sinh kĩ năng suy luận, vận dụng tính chất của hình chữ nhật để chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau, chứng minh ba điểm thẳng hàng, hai đường thẳng song song.
A. Tóm tắt kim chỉ nan
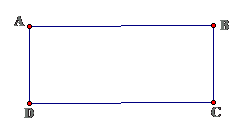
1. Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông
$ \displaystyle \diamond ABCD$ là hình chữ nhật $ \displaystyle \Leftrightarrow \left\{ \begin{array}{l}\diamond ABCD\\\hat{A}=\hat{B}=\hat{C}=\hat{D}\end{array} \right.$
– Nhận xét : Hình chữ nhật cũng là 1 hình bình hành, 1 hình thang cân
2. Tính chất: Hình chữ nhật có tất cả các tính chất của hình bình hành và hình thang cân
– Tính chất về cạnh: Các cạnh đối bằng nhau, song song với nhau
– Tính chất về góc: Bốn góc bằng nhau
– Tính chất về đường chéo: Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
3. Dấu hiệu nhận biết
– Tứ giác có ba góc vuông là hình chữ nhật
– Hình thang cân có 1 góc vuông là hình chữ nhật
– Hình bình hành có 1 góc vuông là hình chữ nhật
– Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
4. Ứng dụng vào tam giác vuông
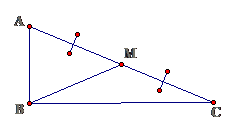
– Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền, ta có: $ \displaystyle BM=\frac{1}{2}AC$– Nếu một tam giác có đường trung tuyến ứng với 1 cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông : $ \ displaystyle BM = \ frac { 1 } { 2 } AC \ Rightarrow \ Delta ABC $ vuông .
B. Bài tập và những dạng toán
Dạng 1 : Chứng minh 1 tứ giác là hình chữ nhật
Cách giải : Vận dụng những tín hiệu nhận ra để chứng tỏ 1 tứ giác là hình chữ nhật
Bài 1: Cho tứ giác ABCD có $ \displaystyle AC\bot BD\equiv O$. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng:
a. OE + OF + OG + OH bằng nửa chu vi tứ giác ABCDb. Tứ giác EFGH là hình chữ nhật
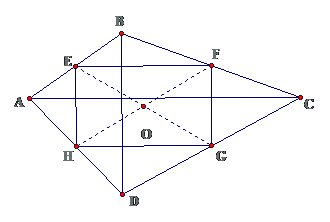
Lời giải
a. Ta có
USD \ displaystyle OE + \ text { OF + OG + OH = } \ frac { \ text { 1 } } { \ text { 2 } } ( AB + BC + CD + DA ) = \ frac { 1 } { 2 } { { P } _ { ABCD } } $
b. Có $ \displaystyle \left\{ \begin{array}{l}\text{EF//GH}\\\text{EF=G}\end{array} \right.\Rightarrow \diamond \text{EFGH}$ là hình bình hành ( dấu hiệu nhận biết )
Mặt khác $ \displaystyle \left\{ \begin{array}{l}AC\bot BD\\AC//\text{EF}\end{array} \right.\Rightarrow \left\{ \begin{array}{l}\text{EF}\bot \text{BD}\\\text{BD//EH}\end{array} \right.\Rightarrow EH\bot \text{EF}\Rightarrow \diamond \text{EFGH}$ là hình chữ nhật (dhnb)
Bài 2: Cho tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC ( M thuộc AB ). Chứng minh tứ giác PCQM là hình chữ nhật.
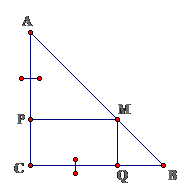
Lời giải
Ta có $ \displaystyle \Delta ABC$ vuông cân $ \displaystyle \Rightarrow \hat{A}={{45}^{0}}\Rightarrow \Delta APM$ vuông cân $ \displaystyle \Rightarrow AP=PM$
Theo giải thiết $ \ displaystyle AP = CQ \ Rightarrow PM = CQ $Lại có $ \ displaystyle PM / / CQ \ Rightarrow \ diamond PMCQ $ là hình bình hànhMặt khác $ \ displaystyle \ hat { C } = { { 90 } ^ { 0 } } \ Rightarrow \ diamond PMCQ $ là hình chữ nhật ( dhnb )
Bài 3: Cho hình chữ nhật ABCD, E thuộc AD, F thuộc AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, DF, BE, BD. Chứng minh rằng IN = KM.
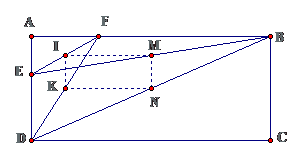
Lời giải
Ta đi chứng minh tứ giác IKMN là hình chữ nhật
+ ) Theo giả thiết có : $ \ displaystyle \ left \ { \ begin { array } { l } IM / / KN ( / / FB ) \ \ IM = KN = \ frac { 1 } { 2 } FB \ end { array } \ right. \ Rightarrow \ diamond IMKN $Là hình bình hành ( dhnb )+ ) $ \ displaystyle \ left \ { \ begin { array } { l } IK / / DA \ \ AD \ bot AB \ end { array } \ right. \ Rightarrow \ left \ { \ begin { array } { l } IK \ bot AB \ \ IM / / AB \ end { array } \ right. \ Rightarrow IM \ bot IK \ Rightarrow \ diamond IKMN $ là hình chữ nhật $ \ displaystyle \ Rightarrow IN = KM USD
Bài 4: Cho tam giác ABC vuông tại A, AB < AC, đường cao AH. Lấy điểm E trên cạnh AC sao cho AE = AB. Gọi I là trung điểm của BE, kẻ $ \displaystyle EK\bot BC(K\in BC),EN\bot AH(N\in AH)$.
a. Chứng minh tứ giác NEKH là hình chữ nhậtb. $ \ displaystyle I \ hat { H } A = I \ hat { H } C USD
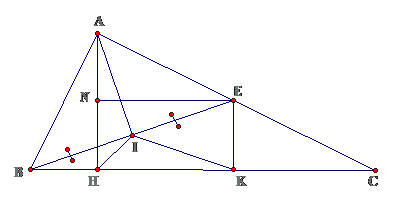
Lời giảia. Tứ giác NEKH có 3 góc vuông nên là hình chữ nhật
b. Ta đi chứng minh $ \displaystyle \Delta IHA=\Delta IHK$
Xét $ \displaystyle \Delta IHA,\Delta IHK:$ IH cạnh chung, $ \displaystyle AI=IK=\frac{1}{2}BE$
Cần thêm AH = HK hoặc AH = NE ( do HK = NE )USD \ displaystyle \ Delta ABH = \ Delta AEN ( ch-gn ) \ Rightarrow AH = NE $⇒ $ \ displaystyle AH = HK \ Rightarrow \ Delta IHA = \ Delta IHK \ Rightarrow I \ hat { H } A = I \ hat { H } C USD
Dạng 2 : Vận dụng đặc thù của HCN để chứng tỏ qua hệ bằng nhau, song song, vuông góc, tính độ dài những đoạn thẳng
Cách giải : Áp dụng những đặc thù của hình chữ nhật– Áp dụng đặc thù đường trung tuyến trong tam giác vuông
Bài 5: Cho hình chữ nhật ABCD, AB = 40cm, O là giao điểm của hai đường chéo. Gọi H là chân đường vuông góc kẻ từ A đến BD. Tính độ dài đoạn DH, OH, OB.
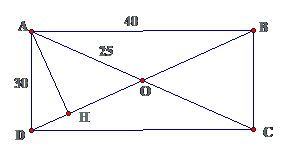
Lời giải
Áp dụng định lý pytago $ \displaystyle \Rightarrow BD=50cm$
USD \ displaystyle OA = OB = OC = OD = 25 cm USD$ \ displaystyle A { { D } ^ { 2 } } – D { { H } ^ { 2 } } = A { { H } ^ { 2 } } = A { { O } ^ { 2 } } – H { { O } ^ { 2 } } = A { { O } ^ { 2 } } – { { ( D { { O } ^ { 2 } } – DH ) } ^ { 2 } } $Hay $ \ displaystyle \ begin { array } { l } { { 30 } ^ { 2 } } – D { { H } ^ { 2 } } = { { 25 } ^ { 2 } } – { { ( 25 – DH ) } ^ { 2 } } \ Leftrightarrow { { 30 } ^ { 2 } } – D { { H } ^ { 2 } } = { { 25 } ^ { 2 } } – ( 625 – 50DH + D { { H } ^ { 2 } } ) \ Leftrightarrow 50DH = 900 \ \ \ Rightarrow DH = 18 \ Rightarrow HO = 7CM \ end { array } $Cách 2 :USD \ displaystyle { { S } _ { ABD } } = \ frac { 1 } { 2 } AD.AB = 600 = \ frac { 1 } { 2 } AH.BD $⇒ $ \ displaystyle 600 = \ frac { 1 } { 2 }. 50. AH \ Rightarrow AH = 24 \ Rightarrow DH = 18 cm USD
Bài 6: Cho hình chữ nhật ABCD. Gọi E là chân đường vuông góc kẻ từ B đến AC. I là trung điểm của AE, M là trung điểm của CD, H là trung điểm của BE.
a. Chứng minh rằng CH / / IMb. Tính góc BIM
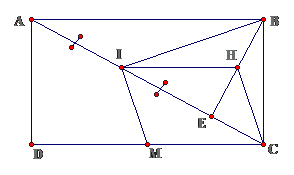
Lời giải
a. Ta có IH là đường trung bình $ \displaystyle \Delta AEB\Rightarrow \left\{ \begin{array}{l}IH//AB\\IH=\frac{1}{2}AB\end{array} \right.$
Lại có $ \ displaystyle \ left \ { \ begin { array } { l } MN / / AB \ \ MN = \ frac { 1 } { 2 } AB \ end { array } \ right. \ Rightarrow \ diamond IMCH $ là hình bình hành $ \ displaystyle \ Rightarrow CH / / IM $Ta có : $ \ displaystyle IH / / MC, MC \ bot BC \ Rightarrow IH \ bot BC $Xét $ \ displaystyle \ Delta IBC $ có H là trực tâm $ \ displaystyle \ Rightarrow \ left \ { \ begin { array } { l } CH \ bot BI \ \ CH / / IM \ end { array } \ right. \ Rightarrow B \ hat { I } M = { { 90 } ^ { 0 } } $
Bài 7: Cho hình chữ nhật ABCD. Lấy điểm P tùy ý trên đường chéo BD. Gọi M là điểm đối xứng của C qua P.
a. Chứng minh AM / / BDb. Gọi E, F lần lượt là hình chiếu của M trên AD, AB. Chứng minh AEMF là hình chữ nhậtc. EF / / ACd. E, F, P thẳng hàng
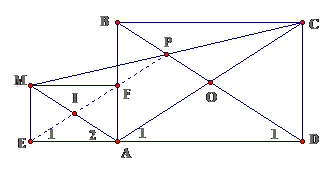
Lời giảia. Gọi O là giao điểm của BD và ACTa có OP là đường trung bình của $ \ displaystyle \ Delta AMC \ Rightarrow OP / / AM USDb. Xét $ \ displaystyle \ diamond AEMF $, có $ \ displaystyle \ hat { E } = \ hat { A } = \ hat { F } = { { 90 } ^ { 0 } } \ Rightarrow \ diamond AEMF $ là hình chữ nhậtc. Ta có $ \ displaystyle { { \ hat { A } } _ { 2 } } = { { \ hat { D } } _ { 1 } } ( slt ), { { \ hat { A } } _ { 2 } } = { { \ hat { E } } _ { 1 } }, { { \ hat { E } } _ { 1 } } = { { \ hat { A } } _ { 1 } } ( dvi ) \ Rightarrow { { \ hat { E } } _ { 1 } } = { { \ hat { A } } _ { 1 } } \ Rightarrow \ text { EF / / AC } $d. E, F, P thẳng hàng $ \ displaystyle IE / / AC, \ text { IP / / AC } \ Leftarrow $ IP là đường trung bình $ \ displaystyle \ Delta AMC $Lại có EF / / AC $ \ displaystyle \ Rightarrow IE / / AC USDTheo tiên đề Ơclit thì E, F, P thẳng hàng
Bài 8: Cho tam giác ABC cân tại A. Từ điểm D trên đáy BC kẻ đường vuông góc với BC cắt AB ở E và AC ở F. Vẽ các hình chữ nhật DBHE và CDFK. Gọi I là tâm của hình chữ nhật BDEH, J là tâm của hình chữ nhật CDFK. Chứng minh rằng:
a. AIDJ và AHIJ là những hình chữ nhậtb. A, H, D thẳng hàng và A là trung điểm của HK
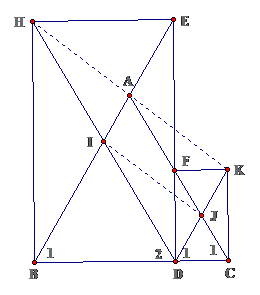
Lời giải
a. $ \displaystyle \diamond AIDJ$là hình bình hành $ \displaystyle \Rightarrow \left\{ \begin{array}{l}AI//DJ({{{\hat{B}}}_{1}}={{{\hat{D}}}_{1}}={{{\hat{C}}}_{1}})\\\text{AJ//DI(}{{{\text{\hat{C}}}}_{\text{1}}}={{{\hat{D}}}_{2}}={{{\hat{B}}}_{1}})\end{array} \right.$
$ \displaystyle \diamond AH\text{IJ}$là hình bình hành $ \displaystyle \Rightarrow \left\{ \begin{array}{l}HI//AJ(HD//AC)\\\text{AJ//HI(=ID})\end{array} \right.$
b. $ \ displaystyle A, H, K $ thẳng hàng $ \ displaystyle \ Rightarrow \ diamond \ text { AIJK } $ là HBH $ \ displaystyle \ Rightarrow \ left \ { \ begin { array } { l } AI / / KJ ( AI / / DJ ) \ \ AI = KJ ( AI = DJ ) \ end { array } \ right. $
Vậy qua A có HA // IJ, KA // IJ nên A, H, K thẳng hàng.
Xem thêm: Thiết lập góc nhìn đa chiều – Duy Tân
Dạng 3 : Sử dụng định lý thuận và hòn đảo của đường trung tuyến ứng với cạnh huyền trong tam giác vuông
Cách giải : Sử dụng định lý về đặc thù đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng tỏ những hình bằng nhau hoặc chứng tỏ tam giác vuông
Bài 9: Cho tam giác ABC, các đường cao BD và CE. Gọi M, N là chân các đường vuông góc kẻ từ B, C đến DE. Gọi I là trung điểm của DE, K là trung điểm của BC. Chứng minh rằng:
a. $ \ displaystyle IK \ bot ED $b. EM = DN
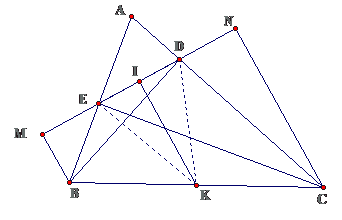
Lời giảia. Ta có $ \ displaystyle EK = DK = \ frac { 1 } { 2 } BC \ Rightarrow \ left \ { \ begin { array } { l } \ Delta EKD ( KE = KD ) \ \ IE = ID \ end { array } \ right. $USD \ displaystyle \ Rightarrow IK \ bot ED ( dpcm ) USDb. $ \ displaystyle \ left \ { \ begin { array } { l } KB = KC ( K \ in BC ) \ \ KI / / BM / / NC \ end { array } \ right. \ Rightarrow KI $ là đường trung bình của hình thang MBNC $ \ displaystyle \ Rightarrow \ left \ { \ begin { array } { l } IM = IN \ \ IE = ID \ end { array } \ right. \ Rightarrow ME = DN USD
Bài 10: Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:
a. $ \ displaystyle I \ hat { H } K = { { 90 } ^ { 0 } } $b. Chu vi tam giác IHK bằng nửa chu vi tam giác ABC
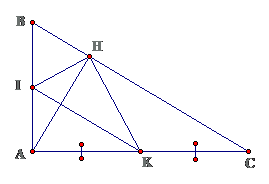
Lời giảia. Ta có : $ \ displaystyle \ Delta IAH, \ Delta KAH $ cân tại I và K $ \ displaystyle \ Rightarrow I \ hat { A } H = I \ hat { H } A, H \ hat { A } K = A \ hat { H } K USDUSD \ displaystyle \ Rightarrow I \ hat { H } A + A \ hat { H } K = { { 90 } ^ { 0 } } \ Rightarrow I \ hat { H } K = { { 90 } ^ { 0 } } $b. Ta có $ \ displaystyle IH = \ frac { 1 } { 2 } AB, HK = \ frac { 1 } { 2 } BC, IK = \ frac { 1 } { 2 } BC \ Rightarrow { { P } _ { IHK } } = \ frac { 1 } { 2 } { { P } _ { ABC } } ( dpcm ) USD
Bài 11: Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của hai tia Ax và By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a. Tứ giác AMBQ là hình gìb. Chứng minh rằng CH vuông góc với ABc. Chứng minh tam giác PIQ cân
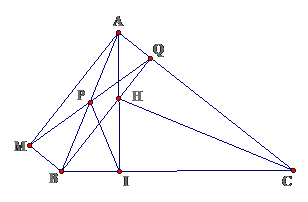
Lời giảia. Ta có tứ giác AMBQ là hình chữ nhật ( hai đường chéo cắt nhau tại trung điểm của mỗi đường và bằng nhau )b. Ta có H là trực tâm của $ \ displaystyle \ Delta ABC \ Rightarrow CH \ bot AB $c. có $ \ displaystyle PI = PQ = \ frac { 1 } { 2 } AB \ Rightarrow \ Delta PIQ $ cân tại P .
Dạng 4 : Tìm điều kiện kèm theo để tứ giác là hình chữ nhật
Cách giải : Vận dụng định nghĩa, những đặc thù và tín hiệu nhận ra của hình chữ nhật
Bài 12: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật.
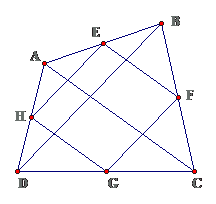
Lời giảiTa có tứ giác EFGH là hình bình hànhĐể EFGH trở thành hình chữ nhật thì :USD \ displaystyle \ Rightarrow H \ text { EF = 9 } { { \ text { 0 } } ^ { \ text { 0 } } } \ Rightarrow HE \ bot \ text { EF } \ Rightarrow \ text { AC } \ bot \ text { BD } $Vậy điều kiện kèm theo là hai đường chéo của tứ giác ABCD vuông góc với nhau .
Bài 13: Cho tam giác ABC. Gọi O là 1 điểm thuộc miền trong của tứ giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB
a. Chứng minh tứ giác MNPQ là hình bình hànhb. Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật
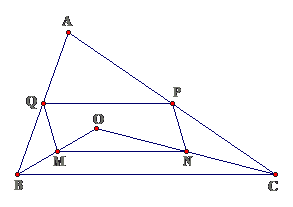
Lời giảia. Ta có MNPQ là hình bình hành ( tín hiệu nhận ra )b. Để MNPQ trở thành hình bình hành thì O nằm trên đường cao xuất phát từ đỉnh A của $ \ displaystyle \ Delta ABC USD
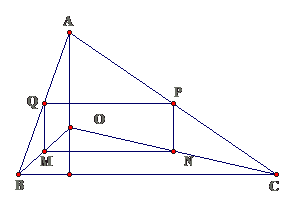
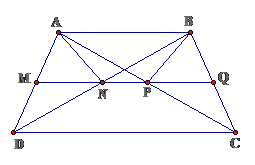
Bài 14: Cho hình thang cân ABCD ( AB // CD, AB < CD ). Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AD, BD, AC, BC
a. Chứng minh bốn điểm M, N, P, Q. thẳng hàngb. Chứng minh tứ giác ABPN là hình thang cânc. Tìm một hệ thức liên hệ giữa AB và CD để ABPN là hình chữ nhật
Lời giải
a. Ta có $ \displaystyle MN//AB,MP//AB,PQ//AB,PN//AB\Rightarrow M,N,P,Q$
thẳng hàng nhau.
b. Hình thang ABPN có hai đường chéo bằng nhau nên là hình thang cânc. Để ABPN là hình chữ nhật thì NP = AB hay CD = 3AB
BÀI TẬP VỀ NHÀ
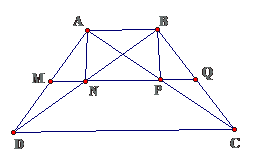
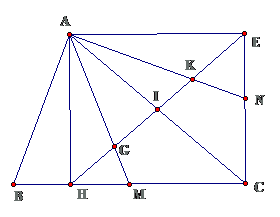
Bài 1: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a. Chứng minh tứ giác AHCE là hình chữ nhậtb. Chứng minh HG = GK = KE
Hướng dẫn
a. Chứng minh tứ giác AHCE là hình bình hành, có
$ \displaystyle AHC={{90}^{0}}\Rightarrow \diamond AHCE$ là hình chữ nhật
b. Chứng minh G, K lần lượt là những trọng tâm của tam giác AHC, AEC và sử dụng đặc thù 2 đường chéo của HCN
Bài 2: Cho tam giác ABC, các đường cao AD, BE, CF cắt nhau tại H, gọi I, K, R theo thứ tự là trung điểm của HA, HB, HC. Gọi M, N, P theo thứ tự là trung điểm của BC, AC, AB. Chứng minh rằng:
a. Tứ giác MNIK, PNRK là những hình chữ nhậtb. P, N, R, K, M, I cùng thuộc 1 đường trònc. D, E, F cũng thuộc đường tròn trên
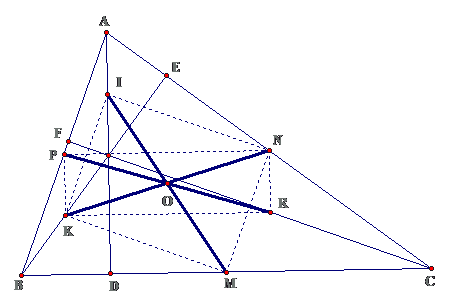
Lời giảiTa có : $ \ displaystyle OD = \ frac { 1 } { 2 } IM, OE = \ frac { 1 } { 2 } KN, \ text { OF = } \ frac { \ text { 1 } } { \ text { 2 } } PR $
Bài 3: Cho tam giác ABC vuông tại A, M thuộc BC. Gọi D và E là chân đường vuông góc kẻ từ M đến AB và AC
a. Định dạng tứ giác ADMEb. Gọi I là trung điểm của DE. Chứng minh A, I, M thẳng hàngc. Điểm M nằm ở đâu trên BC thì DE nhỏ nhất. Tính DE trong trường hợp đó biết AB = 15 cm, AC = 20 cm
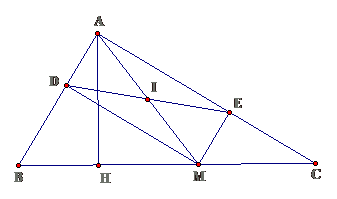
Lời giảia. Tứ giác ADME có 3 góc vuông nên là hình chữ nhật
c. DE nhỏ nhất khi AM nhỏ nhất ( DE = AM ). AM nhỏ nhất khi và chỉ khi AM = AH khi M trùng H
Xem thêm: Hoàng Duy Hùng – Wikipedia tiếng Việt
Xét $ \ displaystyle \ Delta ABC $ vuông tại AUSD \ displaystyle \ Rightarrow BC = 25 cm ( pytago ) \ Rightarrow { { S } _ { ABC } } = \ frac { 1 } { 2 } AH.BC = \ frac { 1 } { 2 } AB.AC \ Rightarrow AH = \ frac { AB.AC } { BC } = \ frac { 15.20 } { 25 } = 12 ( cm ) USDBồi dưỡng Toán 8, Hình học 8 – Tags: hình chữ nhật
Source: https://evbn.org
Category: Góc Nhìn















![Toni Kroos là ai? [ sự thật về tiểu sử đầy đủ Toni Kroos ]](https://evbn.org/wp-content/uploads/New-Project-6635-1671934592.jpg)


